Managed Futures: The Power Of Enhanced Diversification

In the previous two Insights in this series, we focused on the risk of various stock-bond- managed futures portfolios, and examined how much of this risk comes from each of their three component asset classes.1 Based on what we believe are some reasonable assumptions about volatilities and correlations, we first showed that most of the risk of traditional stock-bond portfolios comes from stocks.

For example, 92% of the risk of a 60/40 stock/bond portfolio is contributed by stocks. Diversifying the portfolio by adding managed futures yields some interesting results. As we distribute the risk of the portfolio approximately equally across the three asset classes, it turns out that the risk-adjusted expected return of the portfolio potentially improves. Among the specific hypothetical scenarios we presented, a portfolio with 20/50/30 allocations to stocks/bonds/managed futures turned out to have the highest Sharpe Ratio among portfolios whose allocations to the three asset classes were constrained to add up to 100%. In this final Insight, we explore the possibility and the consequences of relaxing this constraint.

Why Should We Consider Relaxing the 100% Constraint? Can This Be Achieved in Practice?

We have shown, albeit under fairly simplistic assumptions, that a 20/50/30 portfolio may have a higher Sharpe Ratio than most others. However, the fact remains that, in the real world, it is extremely rare to find portfolios with allocations as high as 30% to alternative strategies. In our view, most portfolios continue to be significantly under-diversified, and, in most cases, stocks continue to be the biggest source of risk, their contribution often exceeding 90%. We believe the main reasons for this under-diversification are (i) the historical lack of availability of diversifying strategies, and (ii) when available, the opportunity costs, both real and perceived, of utilizing them.

1. Historical Lack of Availability:

Until quite recently, many diversifying alternative strategies were unavailable to investors other than institutions or ultra-high-net-worth individuals.

Investors perceived these types of investments— which often involve short-selling, use leverage and/or derivatives, and trade illiquid assets—as being either “too risky” or “too complex,” unlike investments in stocks and bonds. Managers of these alternative strategies expected to be paid for their skill in providing uncorrelated, absolute returns streams, and often demanded fees such as “2 and 20,” and performance-based incentive fees were viewed as relatively difficult to accommodate in a mutual fund structure. As a result, these alternative strategies generally remained out of reach for most individual investors, making it difficult for them to diversify meaningfully. For about a decade now, however, many diversifying alternative strategies have been packaged into mutual fund structures, making them more widely available.

2. Opportunity Costs:

With few exceptions, even those investors who have access to “hedge fund strategies” tend to allocate only small amounts to alternatives, so that the equity market remains the largest source of risk in their portfolios. Further, the correlations to equities of many of these strategies increased dramatically during market meltdowns (such as the Global Financial Crisis of 2008). Thus, investments intended to be diversifiers of equity risk ended up displaying equity-like performance at precisely the wrong times. As we have discussed elsewhere2, managed futures was one of the very few strategies that held up well during the Crisis; even so, however, the typical allocation to them—generally below 5%—has almost invariably been too small to make a meaningful difference.

Let us explore this concept of opportunity costs more fully. Consider an investor holding a $1million dollar 60/40 stock/bond portfolio who decides to allocate 20% to managed futures strategies. Traditionally, the way to achieve this is to sell stocks and/or bonds and invest in a mutual fund (or other structure) that accesses the managed futures trading strategies. The managed futures mutual fund, however, typically takes in the $200,000 and holds most of it in the form of cash and equivalents, such as short-maturity Treasury bills. A small part of the $200,000 (usually 10% to 25%) is used as margin or collateral to access the managed futures trading program(s). Thus, a 60/40 portfolio effectively becomes a 48/32/20 stock/ bond/cash portfolio, plus access to a diversifying return stream. If we believe that stocks and bonds in the long run have higher expected returns than cash (which they ought to, because they are riskier), then diversification has been achieved at a significant opportunity cost: exposure to stocks and bonds has been reduced by 20%. The decision has been framed—and implemented—as an “OR” decision: either you can be 20% exposed to stocks and bonds, OR you can be exposed 20% to cash and have 20% “notional exposure” to managed futures trading program(s). This is the opportunity cost, and it increases with the size of the allocation to managed futures.

The “Ampersand” or “The Power of &” solution we propose is simple in theory: there is no need to sell stocks and bonds in order to gain exposure to managed futures trading programs. As these programs can typically be accessed by using anywhere from 10% to 25% margin or collateral, the stocks and/or bonds in the investor’s 60/40 portfolio can themselves be posted as collateral (likely with a small “haircut,” depending on the exact situation). This is an “overlay” approach, where the alternatives are overlaid on top of the stock/bond portfolio without the need to sell any stocks or bonds. We will not go into details here about how exactly this would be implemented, as that would vary from case to case, but we will simply assure the reader that it can indeed be accomplished in practice.

But does this really need to be an “OR” decision? We believe it does not; it can instead be structured as an “AND” proposition: full exposure to stocks and bonds AND the desired, meaningful exposure to managed futures.

The Risk Contribution of Stocks in Portfolios with Enhanced Diversification

Not knowing how volatile stocks, bonds, and managed futures may be in the future, we make some assumptions, as before, that are based roughly on the values realised during the period 1987-2016.3 In Table 1, we show the volatilities we assume for stocks, bonds, and managed futures, as well as our assumed correlations between each pair of asset classes. We also make what we believe are some reasonable assumptions about the long-run expected returns for each asset class: We assume that the risk-free rate of interest will be 1%, and that all three asset classes will have the same Sharpe Ratio going forward.4

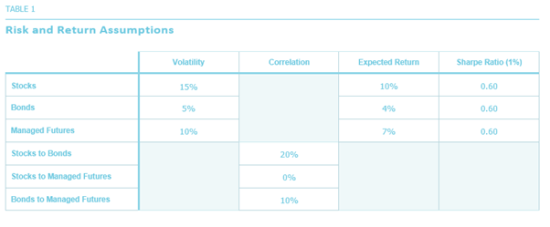
Table 2, we show the risk of portfolios with a range of allocations to stocks and bonds, which add up to 100%, plus an allocation “managed futures,” so that the three allocations may add up to more than 100%. Note that the portfolios at the two upper corners of the table represent portfolios with 100% allocated to bonds (left) or stocks (right). Portfolios in the first row (shaded in green) represent stock/bond portfolios; the blue-shaded portfolios in the first column are bond/managed futures portfolios, while the peach-shaded ones in the last column are stock/ managed futures portfolios. All the others are three-asset portfolios.5 Thus, a 50/50 stock/bond portfolio with an additional 40% exposure to managed futures (shaded in purple) has a risk of 9.4%. Note that this is slightly lower than the risk of a 60/40 stock/bond portfolio, which is 9.6%: an example of the potential benefits of diversification.

Finally, note that we show managed futures exposure ranging from 0% to 150%; our “enhanced diversification” approach can potentially provide notional exposure to managed futures that is significantly higher than 100%.6

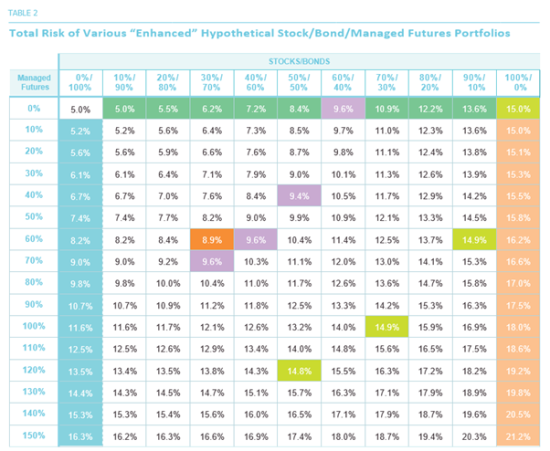
Some other interesting results can be seen in Table 2. Let’s assume that an investor is comfortable with the overall risk of a 60/40 stock/bond portfolio, which is 9.6%. We see from the table that a similar level of risk is associated with “enhanced” portfolios in which part of the 60% stock allocation is replaced by a combination of bonds and managed futures. For example, a 30/70/70 portfolio has approximately the same 9.6% risk level, as do some of the other portfolios (all shaded in purple), such as 40/60/60 or 50/50/40 (which, to be precise, has a slightly lower risk of 9.4%).

Very well, you say. But what about the returns of these so-called “enhanced portfolios” relative to the 60/40 portfolio? Let’s look at the return numbers shown in Table 3.

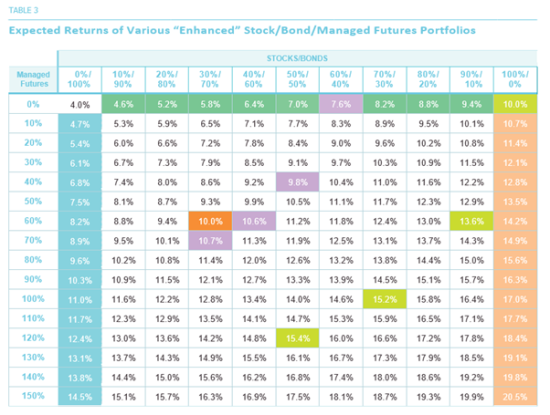
As we discussed in Part 2, the expected return of a portfolio is simply the weighted average of the returns of the component asset classes. Thus, the 50/50/40 portfolio, for example, has expected return equal to the sum of 50% of the expected returns for stocks and bonds (equal to 5% and 2%, respectively), plus 40% of the expected return for managed futures (40% of 7% is 2.8%), which is 9.8%, as shown in the table. This number is 220 basis points higher than the 7.6% return of a 60/40 portfolio. The potential benefit of “enhanced diversification” is that it results in portfolios with the same potential level of risk but with a potentially higher expected return.

The lime green-shaded cells in the upper right-hand corner of Tables 2 and 3 represent a 100% stock portfolio, which has a risk of 15% and an expected return of 10%. When we look at “enhanced portfolios,” we find that the 15% risk level can be (approximately) obtained by holding portfolios (also shaded in lime green) such as 90/10/60, or 70/30/100, or 50/50/120. But in all three of these cases, the expected return of the enhanced portfolio is significantly higher than 10%, the expected return of the 100% stock portfolio.

As we saw in Part 2, one way to combine the information in Tables 2 and 3 is to calculate the Sharpe Ratio for each portfolio. This ratio is simply a measure of how much “risk premium” a portfolio earns per unit of risk that it takes. All else equal, a higher Sharpe Ratio implies a more desirable portfolio.

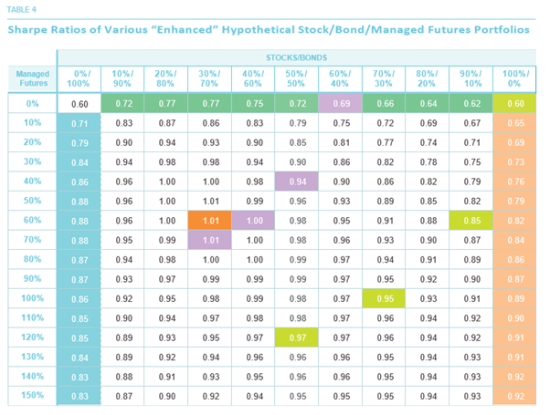
In Table 4, we show the Sharpe Ratios for the various portfolios. The portfolio with the highest Sharpe Ratio, 1.01, turns out to be the 30/70/60 stock/bond/managed futures portfolio, which has an expected return of 10.0% and volatility of 8.9%. This is in some sense the “optimal” or “best” portfolio in terms of the trade-off between risk and return.

Consider the 30/70/60 portfolio from Table 4, which had the highest Sharpe Ratio. It turns out that the risk contributions to this portfolio are: stocks 30%, bonds 22% and managed futures 48%. Since the minimum allocation change considered in Table 4 is 10%, we cannot readily read off from the table a “risk parity” portfolio, where the three asset classes have equal contributions. In fact, the “risk-parity” portfolio turns out to be 76/24/41; this portfolio has a Sharpe Ratio of 1.01, which would be among the high values in Table 4, but not quite the highest. As we cautioned in Part 2, it is not necessary that the risk-parity portfolio be the highest Sharpe Ratio portfolio, or vice versa.

Once again, using some very simple assumptions, we have shown that “well diversified” portfolios, whose risk contributions are more spread out across their component asset classes, typically turn out to have high reward-to-risk ratios. Such portfolios appear to offer better reward to risk trade-offs than portfolios whose risk contributions are more “skewed” towards any asset class(es). This reiterates one of the key teachings of Modern Portfolio Theory (MPT): Diversification helps.

The Potential Benefits of “Enhanced Diversification”

Let’s recap the potential benefits of “enhanced diversification.”

1. Eliminating the opportunity costs of meaningful diversification:

As we discussed, most investors tend to “dip their toe in the water” where diversification is concerned. This is driven at least in part by the fear of having to miss out on stock or bond returns when those assets are sold to diversify into managed futures. “Enhanced diversification” can potentially eliminate these opportunity costs. As shown, a 60/40 portfolio has an expected return of 7.6%, risk of 9.6%, and a Sharpe Ratio of 0.69. A 70/30/70 “enhanced” portfolio with about the same level of risk has an expected return of 10.7% (310 basis points higher) and a Sharpe Ratio of 1.01. Enhanced diversification truly enhances the potential free lunch that diversification provides.

2. Better balanced portfolio construction:

As we (and others) have sought to convey, a “risk parity- based” portfolio, whose component asset classes contribute (about) equally to its overall risk, offers a potentially higher reward-to-risk trade-off. For example, we showed in Part 2 that a 20/50/30 stock/bond/managed futures portfolio has an expected return of 6.1% and risk of 5.4%, for a Sharpe Ratio of 0.95 (using a 1% risk-free rate). This portfolio also has roughly equal risk contributions coming from all three asset classes. If an investor were to stick to just stocks and bonds but seek a “risk parity- based” approach, she would end up with approximately a 25/75 stock/bond portfolio, with an expected return of about 5.6% and a Sharpe Ratio of around 0.75. Clearly, meaningful diversification into managed futures already has potentially large benefits. However, enhanced diversification appears to truly “enhance” these potential benefits, as we discussed in the previous bullet point: an expected return of 10.7% with a Sharpe Ratio of 1.01 for an enhanced, risk parity-based portfolio looks far more attractive.

3. Higher potential returns for investors with higher risk tolerance:

While a higher Sharpe Ratio is generally desirable, all portfolios with the same Sharpe Ratio are not necessarily equivalent. Consider Portfolio A, with an expected return of 6% and risk of 5%, and Portfolio B, with an expected return of 16% and risk of 15%. Although both portfolios have the same Sharpe Ratio, which is 1.00, an investor who is willing to take on more risk (a 35-year-old investment banker, for example) might prefer Portfolio B, while an older and more risk-averse investor (a retired school teacher) might prefer Portfolio A. In Part 2, we discussed how MPT suggests that investors combine a “tangency portfolio” with risk-free lending or borrowing to end up with an overall portfolio still with the highest possible Sharpe Ratio, but with the risk level appropriate for their risk preferences. Investors with higher risk aversion would combine the market portfolio with risk-free lending while less risk-averse investors could, in theory, borrow at the risk-free rate and leverage the risky portfolio to arrive at an appropriate level of risk.7

In our example, if risk-free borrowing were available, Portfolio A could be leveraged by borrowing 200%; the leveraged portfolio’s returns would be identical to Portfolio B’s. Risk-free borrowing of 200% is generally not available to individual investors. An “enhanced” portfolio could potentially play the role of such a leveraged portfolio (see the figure below).

One constraint that MPT imposes on the tangency portfolio is that the allocations sum up to 100%, even when borrowing or lending is involved. In this Insight, we have effectively shown that enhanced diversification, where portfolio allocations are “unconstrained” and can add up to more than 100%, can be used to construct portfolios resembling those suggested by MPT. In the diagram below, we show the “efficient frontier” of diversified portfolios (green/orange) along with the efficient frontier resulting from enhanced diversification (blue/black).

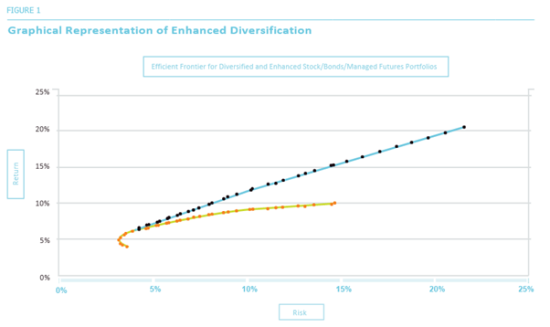
Note that the “enhanced” efficient frontier dominates the other: Any given level of risk is associated with a higher potential expected return. For example, at a risk level of 10%, a “traditional” diversified portfolio (with allocations adding up to 100%) has an expected return of about 8.8%, much lower than the enhanced portfolio’s expected return of about 11.1%. Thus, enhanced diversification, by harnessing “The Power of &,” may effectively offer investors both a higher risk and a higher expected return. This is the equivalent of moving up and down the risk spectrum by either lending or borrowing at the risk-free rate.8

Extended diversification may enable investors to potentially harness the combined benefit of their current portfolio AND managed futures. The traditional “OR” decision involves selling parts of existing stock and/or bond holdings to gain exposure to a diversifying asset class such as managed futures; the decision thus implies explicitly choosing between managed futures OR stocks and bonds. Thus, the traditional method of allocation to managed futures incurs the opportunity cost of forgoing the returns that the stocks and bonds might have continued to earn. Extended diversification seeks to allow investors to hold on to their stocks and bonds AND allocate to managed futures without the opportunity cost of selling stocks and bonds. In many cases, by managing allocations appropriately, this can potentially be achieved without taking on the significant increase in risk experienced by a portfolio that is leveraged traditionally through borrowing.9

Dr Ajay Dravid is the Chief Investment Officer of Equinox Institutional Asset Management. This article is an abridged version of The Risk Contribution of Stocks.

Footnotes

1 The Risk Contribution of Stocks, Parts 1 and 2. We use the standard deviation of returns, also called volatility, as a measure of risk. For most traditional assets, and when dealing with returns measured over reasonably long horizons, volatility serves as an adequate proxy for risk

2 See our Insight, Managed Futures During Equity “Crises” - An Update for more on this discussion

3 For the sake of consistency, we use the same values as in the previous two insights. Please note that past performance is not indicative of future results.

4 We discuss Sharpe Ratio later in the paper. This assumption of equal Sharpe Ratios has the effect of seeking to minimize the bias in favour of any asset class. The expected returns we assume are loosely based on their historical realized values. The substantive conclusions of this Insight do not depend on the assumptions, however.

5 The green-shaded numbers are identical to those shown in our previous insight.

6 For CTA programs, “notional exposure” is a tricky concept, as we have discussed elsewhere; for example, see our 2017 insight, “Managed Futures: Risk Management in CTA Programs.” $30MM of notional exposure to a CTA’s 1X program entails the same risk as $10MM of notional exposure to that CTA’s 3X program.

7 Of course, these prescriptions are based on several simplifying assumptions, many of which are not necessarily reflective of financial markets in practice.

8 The futures markets offer investors implicit “borrowing” or “leverage,” generally at a reasonable spread above the risk-free rate, since futures contracts can be traded by posting a small amount of margin or collateral, in contrast to fully-funded cash purchases. See also footnote 9.

9 This may be possible for an asset class such as managed futures, where only a small amount of margin or collateral needs to be posted to gain exposure to trading programs. As we have discussed, extended diversification potentially affords investors the opportunity to post their existing stocks and bonds as collateral rather than having to sell them.

***

The views expressed in this article are those of the author and do not necessarily reflect the views of AlphaWeek or its publisher, The Sortino Group